如果你也在 怎样代写复杂网络Complex Network TSKS33这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。复杂网络Complex Network在网络理论的背景下,复杂网络是指具有非微观拓扑特征的图(网络)–这些特征在简单的网络(如格子或随机图)中不会出现,但在代表真实系统的网络中经常出现。复杂网络的研究是一个年轻而活跃的科学研究领域(自2000年以来),主要受到现实世界网络的经验发现的启发,如计算机网络、生物网络、技术网络、大脑网络、气候网络和社会网络。
复杂网络Complex Network大多数社会、生物和技术网络显示出实质性的非微观拓扑特征,其元素之间的连接模式既不是纯粹的规则也不是纯粹的随机。这些特征包括学位分布的重尾、高聚类系数、顶点之间的同态性或异态性、社区结构和层次结构。在有向网络的情况下,这些特征还包括互惠性、三联体重要性概况和其他特征。相比之下,过去研究的许多网络的数学模型,如格子和随机图,并没有显示这些特征。最复杂的结构可以由具有中等数量相互作用的网络实现。这与中等概率获得最大信息含量(熵)的事实相对应。
复杂网络Complex Network代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的复杂网络Complex Network作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此复杂网络Complex Network作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
海外留学生论文代写;英美Essay代写佼佼者!
EssayTA™有超过2000+名英美本地论文代写导师, 覆盖所有的专业和学科, 每位论文代写导师超过10,000小时的学术Essay代写经验, 并具有Master或PhD以上学位.
EssayTA™在线essay代写、散文、论文代写,3分钟下单,匹配您专业相关写作导师,为您的留学生涯助力!
我们拥有来自全球顶级写手的帮助,我们秉承:责任、能力、时间,为每个留学生提供优质代写服务
论文代写只需三步, 随时查看和管理您的论文进度, 在线与导师直接沟通论文细节, 在线提出修改要求. EssayTA™支持Paypal, Visa Card, Master Card, 虚拟币USDT, 信用卡, 支付宝, 微信支付等所有付款方式.

数据科学代写|复杂网络代写Complex Network代考|Avalanches and cascading failures
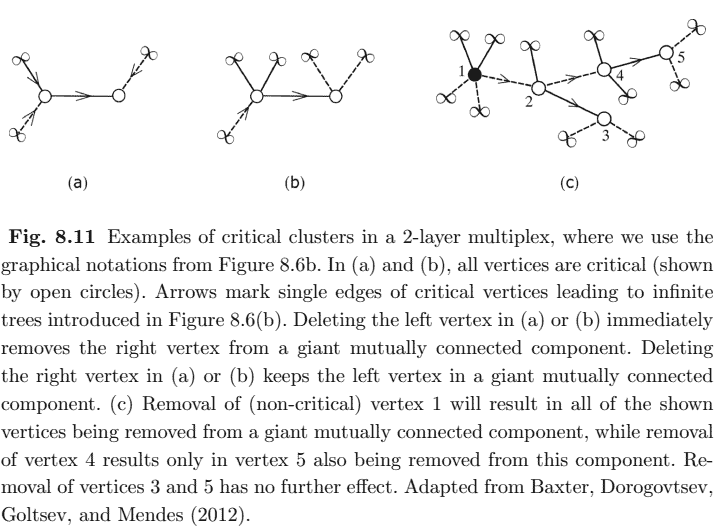
When considering a hybrid transition associated with the emergence of a $k$-core in one-layer networks in Section 6.7, we paid particular attention to its weakest, critical part, namely its corona, easily collapsing and producing large avalanches near the transition. A giant mutually connected component in interdependent networks contains a similar critical subgraph. For the sake of clarity, we focus on locally tree-like multiplex networks. Let us introduce critical vertices in a giant mutually connected component. By definition, these vertices have exactly one edge in one of the layers (colours) of the multiplex leading to an infinite tree of the kind introduced in Figure 8.6b. In addition, they must have at least one edge in each of the remaining layers (colours), leading to the infinite trees of this kind. One can indicate such single edges connecting the infinite trees of Figure $8.6 \mathrm{~b}$ to critical vertices in a multiplex by arrows as is shown in Figure 8.11. This figure explains that the direction of each of such edges is unique. Note that the source vertex of a ‘directed’ edge can be either critical or non-critical, belonging to a giant mutually connected component. The set of these ‘directed’ edges with their end vertices, critical and non-critical, form the critical subgraph of a giant mutually connected component. This subgraph in its turn contains numerous separate finite critical clusters. Removal of a vertex in a critical cluster results in the removal of all downstream critical vertices, that is, in the avalanche transmitted in the direction of the arrows. These avalanches can produce new critical vertices, creating a substrate for next avalanches.
数据科学代写|复杂网络代写Complex Network代考|Other percolation problems
The definition of a mutually connected component containing the requirement that its vertices must be connected by paths within each of $M$ layers of an interdependent network implies the increasing with $M$ number of conditions, which leads to a threshold diverging as $M$ approaches infinity. Radicchi and Bianconi (2017) introduced a percolation problem for multilayer networks, without such a divergence. The idea was to reduce from $M$ to 2 the number of required paths running within different layers between each two vertices in a component. Here we indicate two options, for the sake of brevity focusing on $M$-layer multiplex networks. (i) In a 2-layer connected component each two vertices are connected by continuous paths within at least two layers (at least one path in one layer and at least one path in another layer). (ii) In a redundant mutually connected component each two vertices are connected by at least one path within a given layer (say, layer 1) and at least one path running within any other layer. Radicchi and Bianconi (2017) explored option (ii). Let us analyse equations for the giant components in these problems. We consider an infinite uncorrelated $M$-layer multiplex described by its joint degree distribution $P\left(q_1, \ldots, q_M\right)$ and use the local tree-likeness of this network. Figure $8.12$ explains the equations in the case of $M=3$. Note that the equations for the probabilities $Z_\alpha$, $\alpha=1,2, \ldots, M$ coincide for problems (i) and (ii). Consequently the thresholds in these problems coincide. The equations for $Z_\alpha$ have the following form:
$$
\begin{aligned}
& Z_\alpha=\sum_{q_1, \ldots, q_M} \frac{q_\alpha P\left(q_1, \ldots, q_M\right)}{\langle q\rangle}\left[1-\left(1-Z_\alpha\right)^{q_\alpha-1}\right] \
& \times\left.\times 1-\frac{1}{\left(1-Z_\alpha\right)^{q_\alpha}} \prod_{\beta=1}^M\left(1-Z_\beta\right)^{q_\beta}\right],
\end{aligned}
$$
while the expressions of the relative sizes $S_{\mathrm{G} 2 \mathrm{LC}}$ and $S_{\mathrm{GRMC}}$ of a giant 2-layer connected component and a giant redundant mutually connected component, respectively, in terms of the probabilities $Z_\alpha$ (Figure 8.12c, d), can be written as $\begin{aligned} & S_{\mathrm{G} 2 \mathrm{LC}}=1+\sum_{q_1, \ldots, q_M} P\left(q_1, \ldots, q_M\right) \ & \times \prod_{\alpha=1}^M\left(1-Z_\alpha\right)^{q_\alpha}\left[M-1-\sum_{\beta=1}^M\left(1-Z_\beta\right)^{-q_\beta}\right], \ & S_{\mathrm{GRMC}}=\sum_{q_1, \ldots, q_M} P\left(q_1, \ldots, q_M\right)\left[1-\left(1-Z_1\right)^{q_1}\right]\left[1-\prod_{\beta=2}^M\left(1-Z_\beta\right)^{q_\beta}\right] .\end{aligned}$

复杂网络代写
数据科学代写|复杂网络代写Complex Network代考|Avalanches and cascading failures
在考虑与出现相关的混合过渡时 $k$-core 在第 $6.7$ 节的一层网络中, 我们特别注意它最薄 弱、关键的部分, 即它的日冕, 容易朋塌并在过渡附近产生大雪崩。相互依赖网络中的 一个巨大的相互连接的组件包含一个相似的关键子图。为了清楚起见, 我们关注局部树 状多路复用网络。让我们在一个巨大的相互连接的组件中引入关键顶点。根据定义, 这 些顶点在多路复用的一层 (颜色) 中恰好有一条边, 导致图 8.6b 中介绍的那种无限 树。此外, 它们必须在乘余的每一层 (颜色) 中至少有一条边, 从而导致这种无限的 树。人们可以指出连接图的无限树的这种单边 $8.6 \mathrm{~b}$ 如图 $8.11$ 所示, 通过箭头指向多路 复用中的关键顶点。该图解释了每条边的方向都是唯一的。请注意, “有向”边的源顶点 可以是关键的或非关键的, 属于一个巨大的相互连接的组件。这些“有向”边及其端点 (临界和非临界) 的集合形成了一个巨大的相互连接的组件的临界子图。该子图又包含 许多独立的有限临界簇。删除关键簇中的顶点会导致删除所有下游关键顶点, 即在箭头 方向传输的雪崩中。这些雪崩可以产生新的关键顶点, 为下一次雪崩创造一个底物。
数据科学代它复杂网络代写Complex Network代考|Other percolation problems
相互连接的组件的定义包含其顶点必须通过每个节点内的路径连接的要求 $M$ 相互依赖的 网络的层数意味着随着 $M$ 条件的数量, 这导致阈值发散为 $M$ 接近无穷大。Radicchi 和 Bianconi (2017) 引入了多层网络的渗透问题, 没有这种分歧。这个想法是减少 $M$ 到 2 在组件中每两个顶点之间的不同层中运行的所需路径数。在这里, 我们指出两个选项, 为了简洁起见, 重点放在 $M$ 层复用网络。(i) 在 2 层连通分量中, 每两个顶点通过至少 两层内的连续路径连接 (一层中至少有一条路径, 另一层中至少有一条路径)。(ii) 在 冗余相互连接的组件中, 每两个顶点通过给定层 (例如, 第 1 层) 内的至少一条路径和 任何其他层内的至少一条路径连接。Radicchi 和 Bianconi (2017) 探讨了选项 (ii)。让 我们分析这些问题中巨大组件的方程式。我们考虑无限不相关 $M$ – 由其联合度分布描述 的层复用 $P\left(q_1, \ldots, q_M\right)$ 并使用该网络的局部树状结构。数字 $8.12$ 在以下情况下解释 方程式 $M=3$. 请注意, 概率方程 $Z_\alpha, \alpha=1,2, \ldots, M$ 问题 (i) 和 (ii) 重合。因此, 这些问题的阈值是一致的。的方程式 $Z_\alpha$ 具有以下形式:
$$
Z_\alpha=\sum_{q_1, \cdots, q_M} \frac{q_\alpha P\left(q_1, \ldots, q_M\right)}{\langle q\rangle}\left[1-\left(1-Z_\alpha\right)^{q_\alpha-1}\right] \quad \times \times 1-\frac{1}{\left(1-Z_\alpha\right)^{q_\alpha}} \prod_{\beta=1}^M
$$
而相对大小的表达式 $S_{\mathrm{G} 2 \mathrm{LC}}$ 和 $S_{\mathrm{GRMC}}$ 一个巨大的 2 层连接组件和一个巨大的冗余相互 连接的组件, 分别在概率方面 $Z_\alpha$ (图8.12c、d), 可以写成
$$
S_{\mathrm{G} 2 \mathrm{LC}}=1+\sum_{q_1, \ldots, q_M} P\left(q_1, \ldots, q_M\right) \quad \times \prod_{\alpha=1}^M\left(1-Z_\alpha\right)^{q_\alpha}\left[M-1-\sum_{\beta=1}^M\left(1-Z_\beta\right)\right.
$$

数据科学代写|复杂网络代写Complex Network代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。